Most decentralized key-value stores use a DHT like Kademlia which results in O(log n) hops for routing. In practice, this is quite slow for latency sensitive DNS-like applications. I haven't come across many solutions that optimize for read performance. The closest is lf by ZeroTier, but it requires all nodes to store the entire key-value set. In this post, we'll explore some ways to do partitioning to reduce the per-node storage demands, and use an on-chain trust anchor such as public keys or a Merkle tree root to authenticate writes. This key-value store could be used for storing records associated with decentralized names off-chain or other applications that only need to store small pieces of information. Compared to blockchains, it offers better scalability, and unlike on-chain updates, we don't need to keep all the historical bloat.

Key properties

1. Decentralized: Any user should be able to spin up a node and contribute to the network, improving fault tolerance and reducing points of failure.
2. On-chain trust anchor: Updates are authenticated using public keys or Merkle tree roots committed on-chain.
3. Eventual consistency: Temporary inconsistencies are acceptable but guarantees that nodes will eventually converge.

Routing & Partitioning

To improve scalability, our key-value store needs to distribute data across multiple nodes. The challenge is achieving this without compromising our "zero-hop" promise. How can we identify which nodes to query when searching for a key's value? To begin, let's examine how the Kademlia Distributed Hash Table (DHT) addresses routing with O(log n) hops.

Kademlia's XOR metric

Each Kademlia node has a routing table. Nodes maintain an <ip address, udp port, node id> triples for peers. Here's how it looks like:

{
  "k_buckets": [
    // K-bucket 0
    [
      {
        "nodeID": "123",
        "ip": "192.168.1.1",
        "port": "8001",
        "lastSeen": "2023-10-07T12:00:00Z"
      }
      // More nodes here...
    ],
    // K-bucket 1
    [
      {
        "nodeID": "789",
        "ip": "192.168.1.2",
        "port": "8002",
        "lastSeen": "2023-10-07T12:01:00Z"
      }
      // More nodes here...
    ]
    // More k-buckets here...
  ]
}

Each node in the Kademlia network is assigned a random ID, 160-bits long if using SHA-1. This bit-length determines the number of k-buckets in the routing table—so, with 160-bit IDs, you'd have 160 k-buckets. There's also the constant k which determines how many peers to store for each k-bucket. This depends on the implementation. For example, IPFS uses k = 20 i.e keeping 20 links/contacts for each k-bucket. The k constant also determines how many replicas should keep a copy of the value for that key.

The notion of "distance" between two nodes in Kademlia is not geographical but rather a bitwise XOR operation on their IDs: d(A,B)=A⊕B. This has some good properties. For instance, the distance from a node to itself is zero d(1111,1111)=0, and it satisfies the triangle inequality d(A,B)≤d(A,C)+d(C,B).

This distance metric enables efficient key lookups. Let's say you're at Node A and are searching for a key located at Node C. You measure the XOR distance between the key and known peers, such as Nodes B and D. If Node B appears closer to the key than Node D, you'd query Node B first. Node B can guide you to even closer nodes, ultimately leading you to Node C, where the key resides. This iterative process minimizes the number of hops needed to find the key.

If you want to store a key-value pair, first the key is hashed producing the same hash length as the node ID. Then, your node would search for the k closest nodes to that hashed key based on the XOR distance metric. The key-value pair would be stored on those k closest nodes to ensure redundancy and availability. When new nodes join or existing ones leave, these key-value pairs may need to be redistributed.

This process of going through multiple hops to find a key adds latency at every step making it unsuitable for our use case.

Consistent Hashing

Distributed key-value stores like Dynamo and Apache Cassandra use consistent hashing to distribute data across shards/partitions. By using the output range of a hash function, it forms "ring," which is treated as a circular space. Nodes are randomly assigned a position in the ring.

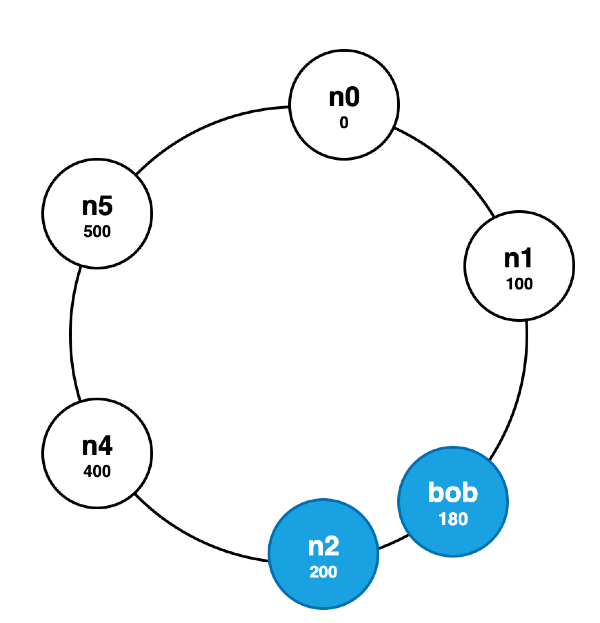
In Fig 1, the hash ring has 5 nodes, each associated with a distinct range of hash values like 0, 100, 200, etc. Assume you have a key called 'bob'. You hash it to get a position on the ring, let's say 180. You move clockwise along the ring until you find a node larger than the key's position. In this example, it would be the node labelled n2 which is responsible for the hash range (101, 200]. Adding a new node only affects its immediate neighbors in the hash ring. This is useful for achieving incremental scalability, as adding or removing a node doesn't necessitate a complete reshuffling of keys. Only the keys that fall into the newly covered hash range will be moved to the new node.

With this approach, we could still reach our O(1) key lookup performance if clients had access to the global routing table and could directly query the node containing their key's value. However, applying this dynamic partitioning approach to uncontrolled, decentralized environments like our key-value store would be quite challenging. Assuming nodes could agree on some mechanism to introduce new partitions, the high volatility of node membership in a P2P network could necessitate frequent key redistributions making the system less stable. We also need to keep the routing table relatively small so clients are able to fetch it.

Hash-based partitioning

Another solution is using a hash function with uniform distribution and mapping its output to the number of shards we need:

ShardId = Hash(key) mod numberOfShards

1. Predictable O(1) key lookups: By sticking to a fixed relatively small number of partitions, clients hold global routing information.
2. No Key Redistribution Needed: In our specific use case, there's no need for key redistribution when nodes join or leave the network. If a particular partition holding your key needs to stay online, it's up to you or neighboring key owners within the same shard to replicate it
3. Flexibility in Replication: Although the number of partitions is fixed, nodes have the flexibility to choose which partitions they wish to replicate. This allows the system to adapt to varying storage and computational capabilities among nodes to some degree.
4. Scalability: Given that Keys are uniformly distributed across partitions, individual nodes need to store a minimum of keys / N , where N is the number of partitions. For instance, if N=500 then for 1 billion keys a single shard only holds ~2 million keys which is not bad!

Here's an example routing table:

{
  "routing_table": [
    {
      "shard_id": 1,
      "peer_nodes": ["node_1", "node_2", "node_7", ...]
    },
    {
      "shard_id": 2,
      "peer_nodes": ["node_1", "node_4", "node_8", ...]
    },
    {
      "shard_id": 3,
      "peer_nodes": ["node_5", "node_6", "node_9", ...]
    },
    // ... up to N
  ]
}

In this design, nodes agree on a fixed number of partitions but have the freedom to replicate any subset. Initially, the system might start by replicating all partitions, allowing nodes to subsequently prune the ones they find less relevant. Increasing the number of partitions improves scalability but makes the routing table larger and the number of peers that clients need to maintain.

Updates, Versioning and Conflicts

An update or a PUT operation could look like the message below. The witness field may be a signature for a public key on-chain for that key's owner or it could be something more advanced like a Merkle proof combined with a signature for a tree root committed on-chain (our design is intentionally blockchain agnostic for now).

{
  "message": {
    "key": "bob",
    "data": "<some_data>",
    "version": 1
  },
  "witness": "<witness-data>"
}

To identify the most recent update, we rely on a version number. Users are free to choose an arbitrary version number but must increment it with each subsequent update. To address the issue of conflicting updates, one solution is to hash the conflicting messages and consider the update with the larger hash value the 'winner.'

State synchronization

Nodes that go offline for an extended period of time will need a way to efficiently identify differences between peer states. To address this, we could use a Merkle tree:

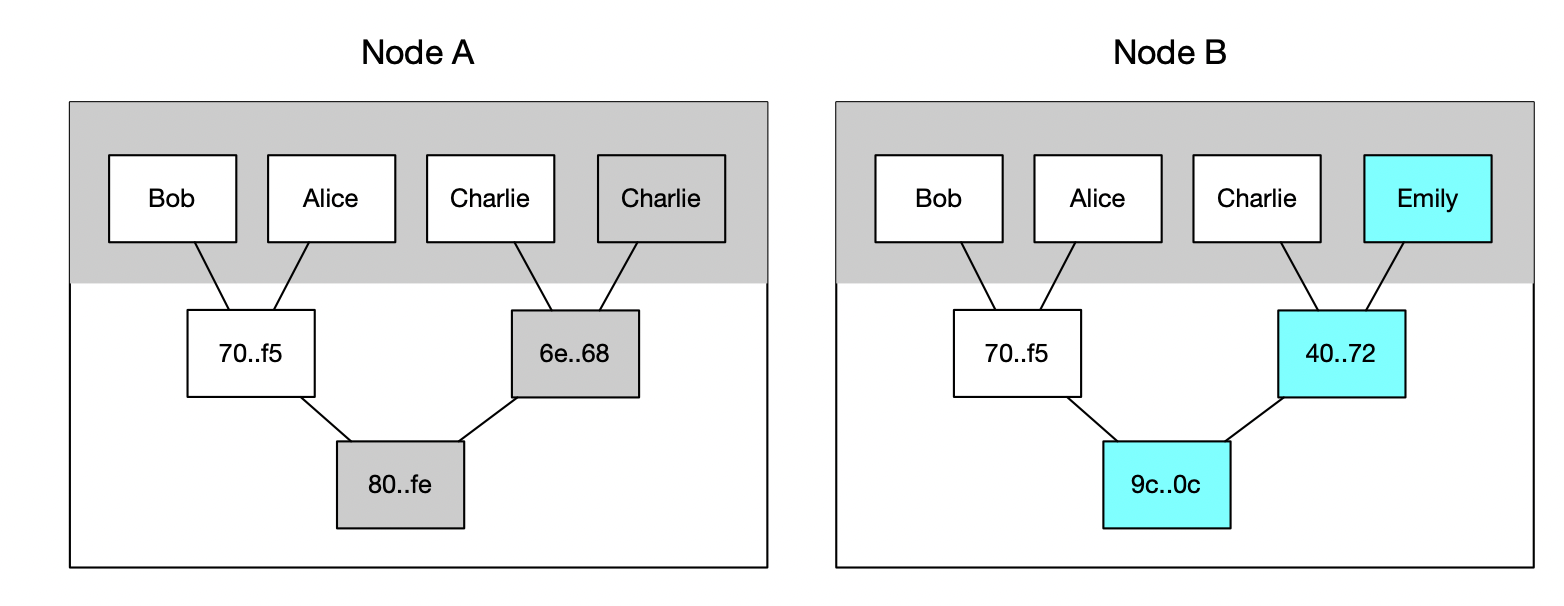
A Merkle tree consists of leaf nodes that hold data blocks, while each non-leaf node is created by hashing its child nodes together. To maintain the structure of a perfect binary tree, odd entries could be duplicated as seen with "Charlie" in Node A. A quick comparison of the root hashes between two trees enables nodes to determine if their states are the same. When a mismatch is found, the nodes engage in a traversal down each branch of the tree, identifying the precise leaves where discrepancies lie. This approach eliminates the need for transferring entire datasets.

So, here's a quirk with this approach: Merkle trees are sensitive to how their leaves are ordered. Imagine two nodes with identical data but shuffled leaf nodes. You'll end up with different root hashes and, consequently, waste time and resources comparing them, only to find out they're the same!

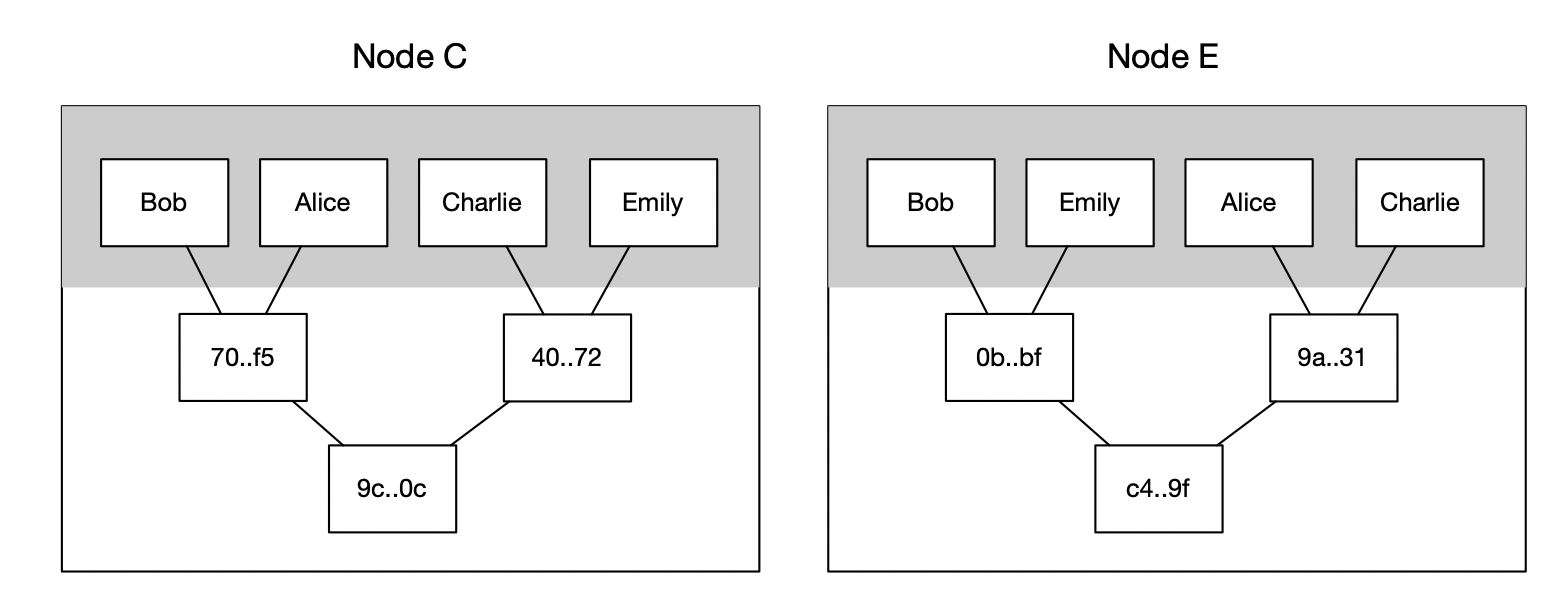
To resolve this, leaves could be sorted. Each time a new entry is added, it needs to be inserted in its sorted position, potentially displacing existing leaves. This not only affects the leaves but also necessitates the recalculation of hashes for the affected branches up the tree. So we should consider some mechanism to do batch updates at regular intervals to minimize this overhead if necessary. Another approach is relying on the order of the keys stored on-chain but this is not always applicable.

Conclusion

In summary, simple hash-based partitioning could be a good compromise between full replication like lf and sacrificing lookup performance by introducing more hops. This approach should in theory scale to 1 billion keys or more. While it's promising, there are still other things that need to be addressed, such as implementing the gossip protocol, protecting against Sybil attacks and other malicious activities in the network. Still, a key-value store with hash based partitioning is quite simple and suitable for DNS-like applications as it offers reliable and predictable lookup performance.

References

https://github.com/zerotier/lf
https://www.allthingsdistributed.com/files/amazon-dynamo-sosp2007.pdf
https://pdos.csail.mit.edu/~petar/papers/maymounkov-kademlia-lncs.pdf
https://docs.ipfs.tech/concepts/dht/